Previous articles have discussed the application of statistics in tolerance analysis: how statistical addition works, how to incorporate the influence of different distributions, and combining worst-case with statistical contributions. The resulting picture is that the outcome of the analysis can depend quite a bit on the assumptions you make. However, as a product designer, you don’t always know in advance with what accuracy the parts will be produced. That makes your analysis as good as the assumptions you make in it. However, if you work with the process capability index Cpk then that will make for a more accurate analysis.
Better Products and Analysis with Process Capability Index Cpk
A great system for controlling dimensional deviations of parts is Six Sigma. An important part in it is the determination of the so-called process capability index Cpk. Parts (products) manufactured with a Cpk requirement (almost) always have dimensional deviations with a Normal (Gauss) distribution. The process capability index Cpk, popularly called ‘the Cpk’, is a measure of the distance of that Normal distribution from the (tolerance) specification. The Cpk can be used for all kinds of parameters in your production process and ultimately leads, among many other things, to a (more) controlled process. Lower failure rate and also more efficient.
The Calculation of the Cpk
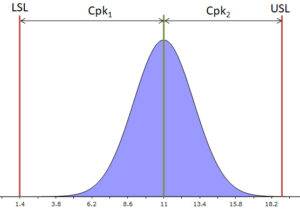
Before we start using the Cpk in the tolerance analysis, first a brief explanation of how the Cpk is calculated. As mentioned, the Cpk says something about the distance of the Normal distribution from the (tolerance) specification. The figure below makes that clear. In it, LSL is the Lower Specification Limit and USL is the Upper Specification Limit. In practice, these are your tolerance limits. Note that the Cpk is the relative distance. In formula form, the Cpk is: Cpk1 = (μ – LSL)/3σ and Cpk2 = (USL – μ)/3σ. With μ = mean value (middle of the Normal distribution) and σ the standard deviation. The smaller value of the two is ‘the Cpk’.
Using Cpk, Do You Have all the Information Now?
So if you know the Cpk of the parts in your tolerance analysis, you can easily use that? The answer is yes and no. Yes, because you can assume that the mean value of all your dimensional deviations are all exactly zero. No, because by doing so you are making another assumption. If the Cpk is known, you don’t yet know what the mean deviation μ is. And you need that in your tolerance analysis.
You can now do two things:
- Pre-specify what the maximum deviation from the mean μ may be.
- Make an assumption regarding the maximum deviation from the mean μ.
Obviously, 1) is preferable. This is because then you know exactly what the possible deviations are. If 1) is not possible, then you will have to make an assumption. That’s not a bad thing, many (manufacturing) companies do that. A commonly used method is the aforementioned Six Sigma method.
Six Sigma Method, a Brief Overview
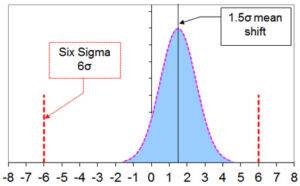
The Six Sigma method was developed by Motorola in 1986, based on observations in their production. In it, they saw that, even in well-controlled processes, the mean values μ showed some drift. And the maximum drift was quantified by Motorola as +/-1.5σ. It may sound odd that the drift of the mean is a factor of the standard deviation σ. But if you think a little longer it actually makes sense. It would be strange if you have a very accurate process, a small σ, with a large drift. And vice versa as well. The name of the method comes from the specification limits: +/-6σ. The figure below depicts that. A Six Sigma compliant process has a Cpk of 1.5 (=(6σ-1.5σ)/3σ).
Interestingly, further, the maximum expected failure rate is 3.4 ppm (3.4 x 10-6). One must keep in mind here that due to drift, only one-sided exceedances of the 6σ limit play a role. And further that the distance from the mean to the 6σ limit is only 4.5σ. If you just want to check this in MS Excel, you can use this formula:
=NORM.DIST(-4.5,0,1,TRUE) or =1-NORM.DIST(4.5,0,1,TRUE).
Using Cpk in Your Tolerance Stack-Up Analysis
So, if the (allowable) mean deviation μ is not known, you can use the value μ=1.5σ like many of other companies. Let’s enter that into the formula for the Cpk and further state that the LSL and the USL are equal to your (symmetric!) tolerance specification ‘Tol’. Then after reworking you get: σ = Tol / (1.5 + 3Cpk). If you do not want to use the factor 1.5 but the factor k (μ=kσ) then you get: σ = Tol / (k + 3Cpk). Since you almost always calculate with 3σ, you still have to multiply this answer by 3.
You now get two columns for each degree of freedom in your tolerance table. One with the 3σ value and one with the expected maximum drift μ. You can easily add up the 3σ values statistically, but how do you add up the individual drift values?
Stack-up Drift in Your Tolerance Table. And put it in a Template!
Drift is often not a phenomenon that averages out easily. So statistical addition is not realistic. On the other hand, worst-case addition is again very pessimistic. It is unlikely that drift will always be maximally unfavorable for all parts in your tolerance chain. So something in between? Yes, something in between seems best. I favor the assumption that the drift μ is randomly distributed for every part in your tolerance chain. Not too optimistic by statistically adding up, nor too pessimistic by considering the drift as worst-case
Randomly distributed is the same as uniformly distributed. And uniformly distributed values may be added statistically with a correction factor. For uniformly distributed values, the correction factor is exactly √3. There is no need to work all that out yourself. All this thinking and calculation is standard in the TolStackUp template, available here on the site.
