With the program HertzWin you can calculate Hertz point and line contacts. The influence of a tangential force can also be calculated. HertzWin is available online for free since March 2009.
No approximation but the exact solution
In older releases of HertzWin (before release 3.1.2) a general approximation formula was used. Starting with release 3.2.0 (December 2020), the situation with gross slip between both bodies can be calculated in detail in HertzWin. This can be done for a circular point contact as well as for a line contact. And as of release 3.4.0 also for an elliptical contact. An overview of the used formulas can be found in the help of the program..
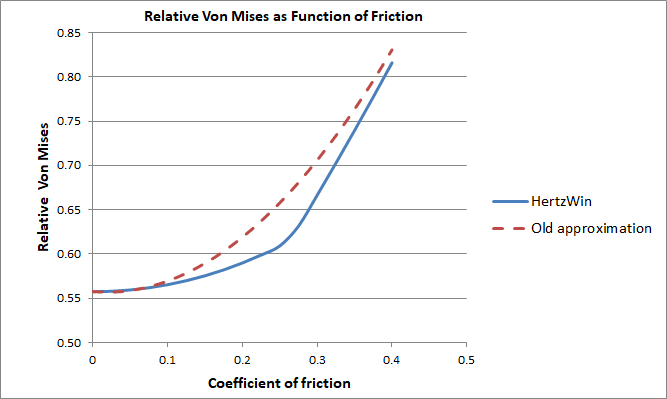
In the figure below, the old approximation in HertzWin is plotted against the coefficient of friction, along with the new, exact method in HertzWin. The vertical axis shows the von Mises stress (vM) as a function of the maximum compressive stress (σHz): vM/σHz. The clearly visible sudden change in the slope of the blue line is the point where the maximum von Mises stress shifts to the surface.
Three Situations: no Slip, Partial Slip or Full Slip
The calculation of a (Hertz) point or line contact subjected to a tangential load is usually divided into three different situations::
- there is no slip between the two bodies (stick);
- there is partial slip between the two bodies;
- the two bodies slide with respect to each other, gross slip.
Applying Tangential Load After the Normal Load
When a tangential load is applied, an interdependence with the normal load is created. Therefore, the calculation is based on the following:
- the normal force is applied first. A small contact area is created which is calculated using the usual Hertz theory;
- then the tangential force is added slowly, increasing slowly from 0 Newton;
- at low values of the tangential force (low in relation to the maximum frictional force), there is almost no slip;
- at higher tangential forces, a slip zone is created at the edge of the contact;
- when the tangential force exceeds the maximum friction, gross slip occurs.
For a normal Hertzian contact, the pressure distribution on the contact surface is quadratic:
![]()
Where: a = half the contact width, x = distance to the center of the contact and σHz = maximum compressive stress at the center of the contact.
Assuming that the (Amonton) law of friction holds at any point on the contact surface, the local tangential force Q(x) (stress) at the surface is given by the following function.
![]()
Where μ is the coefficient of friction. This distribution is used to calculate the effect of gross slip. The next figure shows what the actual force distribution looks like when a tangential force is present.
Elliptical Contact Calculation
Calculations with a tangential force on an elliptical contact are currently not (yet) possible in HertzWin. However, it appears that the differences between a circular contact and a line contact are not very large, see ‘Rough Contact Between Elastically and Geometrically Identical Curved Bodies‘ by Bryant and Keer. If the contact is highly elliptical, the results of a line contact with the same Hertzian compressive stress can be used. If the contact is nearly circular, the results for a circular contact surface can be used. Two extreme examples, both with: Young’s modulus of 200 GPa, Poisson’s ratio of 0.3, and coefficient of friction of 0.2.:
- Line contact, radii 60 mm and 20 mm, contact length 100 mm, normal force 5000 N. This situation results in a Hertzian compressive stress of 341.5 MPa and a maximum von Mises stress of 201.5 MPa. The maximum tensile stress is 136.6 MPa;
- Circular contact, sphere on a flat surface with a sphere radius of 60 mm and a normal force of 61.34 N adjusted to also give a Hertzian compressive stress of 341.5 MPa. The maximum von Mises stress is now 217.7 MPa. Maximum tensile stress is 160.9 MPa..
Between this line contact and the point contact, there is a difference of less than 10% for the von Mises stress and less than 20% for the tensile stress. This is consistent with the conclusions of the Bryant and Keer article. The stresses for an elliptical contact will be in between these results. The direction of the tangential load in an elliptical contact is parallel to the minor axis ‘b’. If the tangential force is parallel to the major axis ‘a’, the estimation errors can be large..
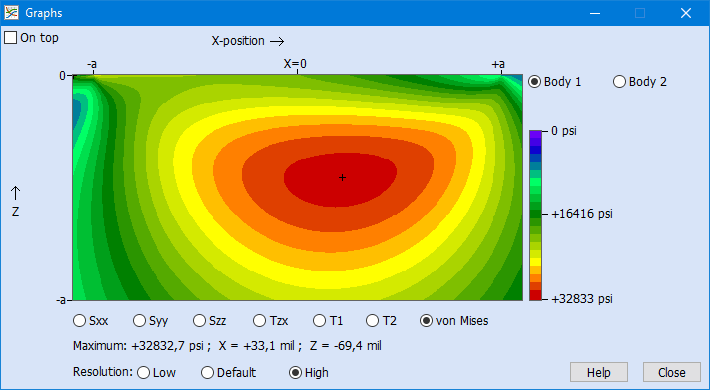
Contour Plot with Colors
HertzWin calculates the material stresses below the contact surface and displays the important stresses (shear, von Mises, and tensile) in the main window. For more insight into the material stresses, you can create contour plots using the Graphs button. Below is an example of a contour plot for a circular point contact with a Poisson’s ratio of 0.3 and a coefficient of friction of 0.2.
Von Mises Stress Shifts to the Surface with High Friction and/or Low Poisson Ratio
As the tangential load increases, the location where the maximum von Mises stress occurs slowly shifts toward the surface. The video below shows the progression with a sliding cylinder (line contact) and increasing coefficient of friction..
Important in this example is the Poisson ratio of 0.3. The moment when the maximum von Mises shifts to the contact surface depends strongly on the Poisson ratio. With a value lower than ~0.2, the maximum von Mises stress is always on the contact surface..
As can be seen, the von Mises stress increases slowly in the beginning: only +1.4% for a friction coefficient of 0.1 and +5.8% for a friction coefficient of 0.2. The closer the von Mises stress is to the surface, the higher the rate of increase. For a friction coefficient of 0.4, the increase is +46.3%..